Building on from this piece on pure versus applied mathematics, we briefly explore the relevance and challenges of mathematics education today and discover ways to re-think and redo learning math in the classroom – a measure we deem imperative to keep up with recent times.
In a study done by Kurt Reusser in 1986, he presented a problem to a group of children: “There are 125 sheep and 5 dogs in a flock. How old is the shepherd?”. His study showed that students’ propensity to reach for an answer at all costs, even when it was insoluble.
Recent research recreated this problem to show that ¾ of children still consider a numerical value to this problem. There appears to be a lack of sense-making among these students in their quest to arrive at a certain value, despite very illogical contexts. Students aren’t provided with enough space to develop intuitions or to think outside of that confined space of the current educational system.
Math has been taught the same way over the past centuries. We saw the age of modern science and technology change how mathematics is needed in daily life, business and society. However, with the rise of the digital age, there becomes a greater need to shift from past practices and thinking to cater to the demands of future.
If we want deeper and more meaningful learning to occur in the field of mathematics education, we need to start asking these fundamental questions: What is the relevance of math in the current times? How can we make math more ‘real’ in the classroom?
With advances made in machine learning and automation, more complex roles will demand more specialized jobs in mathematics, computing and engineering. Alongside this, there will be greater demand for the ability to solve increasingly composite problems across different sectors and industries. In a recent article published by McKinsey, sixty percent of occupations have the potential to be automated by at least 30% based on current demonstrated technologies. Roles will be shifting and more people will be working with technology.
Math’s value and utility will shift to finding patterns, representing these patterns, problem-solving and developing critical, logical and computational thinking. In an article by the World Economic Forum, David Deming, associate professor of education and economics at Harvard, mapped the changing needs of employers and highlighted job skills that will thrive in the future – along with social skills, mathematical ability presented huge benefits.
The role of math in different industries and in real-life is becoming indispensable. In programming, half of job openings are outside the industry of technology. In healthcare, we saw mathematics’ potential in Florence Nightingale’s role as a nurse during the Crimean War. She tapped into statistics when she investigated the unprecedented mortality rate of soldiers in Turkey which she found was not due to war – but sanitation. In his TED Talk and study of community perceptions, Alan Smith stressed the idea that statistics is a study about us. We should be able to look into problems that mean something to us – such as the average amount it takes for us to pay off debt from student loans using the measures of central tendency. If you’re in the renewable energy sector, geometric and trigonometric functions can be used to optimize solar panel placement, or if you’re microfinance and humanitarian work, algebraic equations can be utilized to complete a loan application (Rutschow, Diamond & Serna-Wallender, 2017). It’s also changing industries such as journalism where responsible reporting and proper command of data are reinforcing the very foundation of the role of reports. A person with an economics degree can potentially improve his productivity by being able to program through Python.
Conrad Wolfram, founder of computerbasedmath.org, went further to encourage students to apply the power of calculus to “pick holes in government statistics, design a traffic system or crack secret codes,” instead of going into rote, passive learning.
But what does this mean then for math teaching and learning?
McKinsey agrees that the current educational system doesn’t support the change in the nature of work. “Far too often, students fail to see connections between what they are learning, their communities and a future job that can sustain them,” exclaimed Harriet Sanford, president and CEO NEA Foundation.
We need to transform mathematics education, but where do we begin? Indeed, there are several adjustments we can do to bring higher-order thinking and learning to students, as well as put it in the context of the ‘real world.’
In a study done by Abdulwahed, Jaworski and Crawford in 2012 entitled “Innovative Approaches to Teaching Mathematics in Higher Education: A Review and Critique,” it advocates that the focus of mathematics education should move from traditional to student-centered learning such as inquiry-, problem- or project-based learning that can often be done individually, in smalls groups or in teams. Learning math doesn’t have to be done alone. Social constructivism urges the exchange of knowledge through collaborative activities and tasks.
Inquiry-based mathematics learning is inclined to follow a more conceptual approach while traditional teaching evidently follows a more procedural approach in problem solving. Problem solving encourages students to search for information that stimulate thinking (Mokhtar et al., 2010).
Another approach that you can try in the classroom is the challenge-driven model, where students can be put up against difficult problems and challenges with no established answers. Students draw on many disciplines, work in teams and collaborate with organisations outside of the university sphere. One remarkable thing about this approach is its re-emphasis on the “founding principles of ancient universities” – the focus on questioning rather than answers as the key to deep learning. This can apply for unsolved problems in science or society with the objective of creating new knowledge instead of learning it. If you’re a teacher of mathematics to students with different majors, this might encourage you to look further and encourage your students to solve problems within their industry through math.
Learning occurs much faster and more intensively through the engagement with real-world problems and embedding learning in connections. Practice and theory feed each other with distinct lines of what is learned and how it can be used, alongside this is greater commitment coming from peer pressure, claim Mulgan, Townsley and Price in their report on “The Challenge-driven University: How Real-life Problems Can Fuel Learning.” Problems can have a personal context such as deciding what kind of train ticket to purchase, or managing supermarket spending. These can also be applied with other courses and may require public data from print and online sources.
One of the ways real-world can come into play in math is through authentic learning and assessment. Steve Revington, the pioneer of authentic learning, claims that it is the ideal setting that education requires “to move towards sustainable, meaningful, relevant learning in the 21st century.” Authentic problems focus on real-world contexts outside of the classroom where mathematics becomes useful or applicable to mathematical analysis of social issues.
Let’s have a look at an example below.
You can see a seventh-grade algebra class by Ben Mook following an authentic assessment approach by focusing not on getting the right answer but following the rights steps to get to that answer, identifying common mistakes, and using incorrect work to break down the error in the thought process. In the time of the interview, his class considered the connection of real work and applied the slope formula to a series of stairs to examine if they followed New York City building codes.
His students possess great understanding of this kind of teaching approach, evidenced by this student’s remark: “It’s not like here’s the formula but here’s why the formula works, here’s something to prove it or here’s something you can think about. Their main goal is not to get you to the right answer but to show you how you got there and show that you really put effort into what you’re thinking.”
While we aren’t suggesting that you completely change the curriculum to accommodate mathematical models, the chance to incorporate this to your existing course brings real-world examples to a higher level. It’s also important to note that the application of math problems aren’t automatically mathematical models. Math models are open-ended problems and permit autonomy among students throughout the modelling process of defining the problem, establishing assumptions, data gathering, developing a model, testing the model, analyzing and reporting one’s findings.
Some very prominent universities have started offering subjects and even courses on mathematical modelling such as the universities of Oxford, Birmingham or at RMIT as a subject.
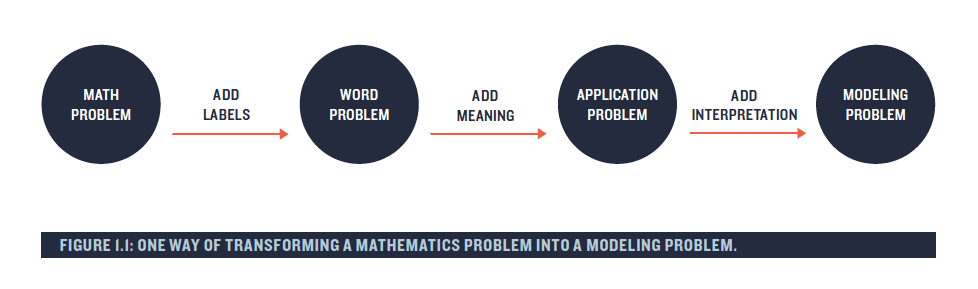
Here is an example problem presented by Consortium for Mathematics and its Applications (COMAP) in the United States in their Guidelines for Assessment & Instruction in Mathematical Modelling Education (GAIMME) report:
Application
Lapse rates can help identify pockets of unstable air and are particularly important for the flight of unmanned aircraft. The lapse rate, y, is defined as rate at which the temperature decreases as altitude increases, or $y=-\frac{d\cdot{T}}{d\cdot{a}}$, where $T$ is the temperature and $a$ is altitude.
The temperature of the atmosphere over Little Rock, Arkansas on a typical October day has been measured and is approximately given by the function:
$T\left(a\right)=23.4-5.81\cdot{a}+0.295\cdot{a}^{2}-0.057\cdot{a}^{3}+0.0024\cdot{a}^{5}+0.006\mathrm{cos}\left(a\right)$, where $T$ is in degrees centigrade and $a$ is in kilometers.
Approximate the lapse rate at a height of 11km by computing the difference quotient with $h=0.1$, $h=0.01$, and $h=0.001$.
Modelling
Lapse rates can help identify pockets of unstable air and are particularly important for the flight of unmanned aircraft. The lapse rate, y, is defined as rate at which the temperature decreases as altitude increases, or $y=-\frac{d\cdot{T}}{d\cdot{a}}$, where $T$ is the temperature and $a$ is altitude.
The temperature of the atmosphere over Little Rock, Arkansas on a typical October day has been measured and is approximately given by the function:
$T\left(a\right)=23.4-5.81\cdot{a}+0.295\cdot{a}^{2}-0.057\cdot{a}^{3}+0.0024\cdot{a}^{5}+0.006\mathrm{cos}\left(a\right)$, where $T$ is in degrees centigrade and $a$ is in kilometers.
You have been asked to assess the safety of a potential drone surveillance mission over the city of Little Rock. The drone is supposed to fly at an approximate height of 11 km over the city, although the mission could be accomplished at any altitude between 9 km and 15 km. Your drone can definitely fly safely if the lapse rate is less than 6C/km; if the lapse rate is over 8C/km, then your drone must be grounded for safety reasons.
Using what you know about difference quotients, assess the safety of the mission and offer a full set of recommendations to your supervisor along with any assumptions you made in completing your analysis.
If you noticed, the application problem on the left does present itself in a real-life context. However, students are unable to give their analysis of the problem back to the context to answer a bigger question, making this a closed problem. On the right-hand side, the problem allows students to show ownership of their decisions by engaging them with the idea of using different quotients to approximate a derivative. Students determine the value of h in this problem. As much as the design and implementation of modelling differs greatly from a traditional course, assessing students under these circumstances are also different. COMAP recommends looking at the student’s ability to evaluate assumptions, provide justifications for those assumptions and assess their mastery of the modelling process. The Society for Industrial and Applied Mathematics conducted a workshop using information from the GAIMME report – have a more in-depth look here.
Linda Shorser released a document on ‘Bloom’s Taxonomy Interpreted for Mathematics’ using the 1st version of the classification. As an educator, this can aid you in ranking your ‘educational objectives’ and support you in creating test questions and homework for your students. As you move higher along the classifications, you’re encouraging higher-level thinking and learning by presenting and applying a variety of exercises. She provides a few examples to guide you through the process:
The New York Times provides some direct examples for introducing applications of algebra. Ultimately, the clamour for higher order thinking and real-world math application has grown in the past decade. With the possibilities of job automation and certain tasks, we need to move deeper into math learning and develop fundamental skills and competencies to prepare our students for the future.
Technology has the capacity to support these developments in mathematics education. Learning environments like SOWISO provide features such as learning analytics, a variety of exercise types and collaborative discussions through the forum to help you organise, structure and assess more meaningful, collaborative and deeper learning.
If you have some ideas or have had experience in making math more ‘real’ in the classroom, we would love to hear it!
Written by Alexis Joson.